1. 그래프란?
그래프란 노드와 연결이 있는 집합체를 말한다.

트리, 연결리스트 등 대부분의 자료구조는 그래프로 이루어져있다고 해도 무방하다.
vertex(정점) : 노드를 가리킨다
edge(간선) : 노드들을 연결하는 선
그래프는 SNS, 지도기능, 라우팅 알고리즘 등 많은곳에서 쓰인다.
어디에서나 사용하고 있다고 봐도 될만큼 쓰임새가 다양하다.
2. 그래프 종류
(1) 무방향 그래프

정점끼리의 간선에 방향이 없는것을 말한다. 방향이 없다는건 양쪽으로 연결되어 있다는 것이다.
(2) 방향 그래프

간선에 방향이 부여되어 있다.
간선은 양쪽을 가리킬수도 있고 한 방향만 가리킬수도 있다.
(3) 비가중 그래프

각 간선에 부여된 값이 없다.
(4) 가중그래프

각 간선에 값이 부여되어 있으며 이를 활용하여 여러가지 로직을 짤수 있다.
걸리는 시간을 최소화 하는 길찾기, 최단경로 계산, 최소 환승 계산 등에 활용한다.
3. 그래프 저장방식
그래프를 저장할때 중요한것은 정점들과 연결을 저장하는 방식이다.
(1) 인접행렬
아래 그림과 같이 행과 열에 맞춰서 정보를 저장한다.
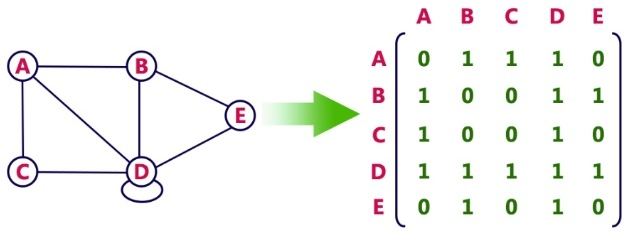
- 간선을 확인하고 싶으면 모든 간선에 대해 루프를 돌아서 찾아야 한다.
- 특정 연결되어있는 간선을 찾는것이 빠르다.
- 공간을 많이 차지한다.
(2) 인접리스트
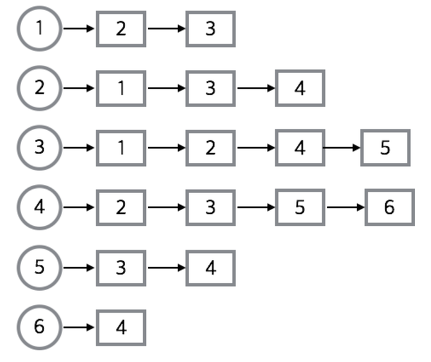
해시테이블을 사용한다.
간선이 많지 않고 퍼져있는 그래프에서는 인접행렬보다 더 적은 공간을 차지한다.
간선을 확인하는것이 인접행렬보다 빠르다.
특정 간선을 찾는것은 순회를 해야하기 때문에 인접행렬보다 느리다
실제로 사용하는 데이터들을 보통 퍼져있는 경우가 더 많기때문에 인접리스트를 사용한다.
4. 인접리스트, 인접행렬 빅O
| v = 정점 e = 간선 | 인접리스트 | 인접행렬 |
| 정점 추가 | O(1) | O(v^2) |
| 간선 추가 | O(1) | O(1) |
| 정점 제거 | O(v+e) | O(v^2) |
| 간선 제거 | O(e) | O(1) |
| query | O(v+e) | O(1) |
| 저장소 | O(v+e) | O(v^2) |
5. 무방향 그래프 구현
(1) 클래스
class Graph {
constructor() {
this.adjacencyList = {};
}
}(2) addVertex (정점추가)
addVertex(vertex) {
if (!this.adjacencyList[vertex]) this.adjacencyList[vertex] = [];
}(3) addEdge (간선추가)
addEdge(v1, v2) {
this.adjacencyList[v1].push(v2);
this.adjacencyList[v2].push(v1);
}(4) removeEdge (간선제거)
removeEdge(vertex1, vertex2) {
this.adjacencyList[vertex1] = this.adjacencyList[vertex1].filter(
(v) => v !== vertex2
);
this.adjacencyList[vertex2] = this.adjacencyList[vertex2].filter(
(v) => v !== vertex1
);
}(5) removeVertex (정점제거)
removeVertex(vertex) {
while (this.adjacencyList[vertex].length) {
const adjacentVertex = this.adjacencyList[vertex].pop();
this.removeEdge(vertex, adjacentVertex);
}
delete this.adjacencyList[vertex];
}6. 그래프 순회
(1) DFS
- 재귀적 방법
depthFirstRecursive(start) {
const result = [];
const visited = {};
const adjacencyList = this.adjacencyList;
(function dfs(vertex) {
if (!vertex) return null;
visited[vertex] = true;
result.push(vertex);
adjacencyList[vertex].forEach((neighbor) => {
if (!visited[neighbor]) {
return dfs(neighbor);
}
});
})(start);
return result;
}- 반복문 사용
depthFirstIterative(start) {
const stack = [start];
const result = [];
const visited = {};
let currentVertex;
visited[start] = true;
while (stack.length) {
currentVertex = stack.pop();
result.push(currentVertex);
this.adjacencyList[currentVertex].forEach((neighbor) => {
if (!visited[neighbor]) {
visited[neighbor] = true;
stack.push(neighbor);
}
});
}
return result;
}(2) BFS
breadthFirst(start) {
const queue = [start];
const result = [];
const visited = {};
visited[start] = true;
let currentVertex;
while (queue.length) {
currentVertex = queue.shift();
result.push(currentVertex);
this.adjacencyList[currentVertex].forEach((neighbor) => {
if (!visited[neighbor]) {
visited[neighbor] = true;
queue.push(neighbor);
}
});
}
}
참고
https://freestrokes.tistory.com/87
'개발 > 자료구조' 카테고리의 다른 글
| [알고리즘] 동적 프로그래밍 (0) | 2022.12.12 |
|---|---|
| [자료구조] 다익스트라 알고리즘 (길찾기) (0) | 2022.12.12 |
| [자료구조] 해시테이블 (0) | 2022.12.06 |
| [자료구조] 우선순위큐 (0) | 2022.12.06 |
| [자료구조] 이진힙 - BinaryHeap (0) | 2022.12.02 |